Нейросетевое приложение для оценивания характеристической экспоненты процесса Леви на примере распределения Бандорффa-Нильсена
Авторы статьи: Белявский Г.И. Пучков Е.В., Лила В.Б.
Введение. Основная задача, которая рассматривается в статье, заключается в построении нейросетевой модели для оценки характеристической экспоненты процесса Леви. Первая работа, связанная с вычислением характеристик случайной последовательности была выполнена в 1949 году Д. Хеббом [1]. Эта работа была связана с решением задачи самообучения нейросети. В последствии было доказано, что алгоритм обучения Д. Хебба непосредственно связан с вычислением главной компоненты. Более эффективный алгоритм обучения сети для вычисления главной компоненты последовательности может быть получен как частный случай метода стохастического градиента [2] с использованием отношения Релея. Если U главный собственный вектор ковариационной матрицы последовательности, то n - е приближение к U вычисляется следующим образом (см., например, [2])
![Z^n = U^{n-1}+h_{n}sign(X^n, U^{n-1})[X^n-(X^n, U^{n-1})U^{n-1}], U^n = \frac{Z^n}{\sqrt{(Z^n,Z^n)}}](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_615ace244222741e19a02684c40b53bd.gif) |
(1) |
В (1) последовательность h удовлетворяет условию: 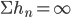 ,
, 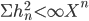 - n-й элемент обучающей выборки.
- n-й элемент обучающей выборки.
Были предложены алгоритмы для определения нескольких главных компонент: (Sanger 1989 [3], Oja 1989 [4] , 1992 [5], Dente and Vilela Mendes 1996 [6]). Для определения нескольких главных компонент можно также использовать метод стохастического градиента. Соответствующий алгоритм вычисления k -главных собственных векторов ковариационной матрицы определяется системой равенств:
![Z^n_1 = U^{n-1}_1+h_{n}^1sign(X^n, U^{n-1}_1)[X^n-(X^n, U^{n-1}_1)U^{n-1}_1], U^{n-1}_1 = \frac{Z^n_1}{\sqrt{(Z^n_1,Z^n_1)}}](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_be5996af173d74b949cd20836bf28813.gif) |
(2) |
![Z^n_2 = U^{n-1}_2+h_{n}^2sign(X^n, U^{n-1}_2)[X^n-(X^n, U^{n-1}_2)U^{n-1}_2], V^{n}_2 = Z^n_2-(Z^n_2, U^n_1)U^n_1, U^n_2 = \frac{V^n_2}{\sqrt{(V^n_2,V^n_2)}}](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_9d49f1ac405d027ec20e6eb265ff7ac2.gif) |
|
| ..... | |
![Z^n_k = U^{n-1}_k+h_{n}^2sign(X^n, U^{n-1}_k)[X^n-(X^n, U^{n-1}_k)U^{n-1}_k], V^{n}_k = Z^n_k-\sum_{i=1}^{k-1}(Z^n_k, U^n_i)U^n_i, U^n_k = \frac{V^n_k}{\sqrt{(V^n_k,V^n_k)}}](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_4bd051fb3018acf1802b506b95377a3e.gif) |
Обоснование алгоритма и доказательство сходимости можно найти в [2]. Если многомерный закон распределения последовательности нормальный с нулевым математическим ожиданием, то ковариационная матрица содержит полную информацию о законе распределения и использование метода главных компонент является оправданным. Если закон распределения не является нормальным, то метод главных компонент является неполным, поскольку не учитывает полностью информацию о поведении данных, например, связанную с моментами порядка три и более. Известен ряд работ (Softy and Kammen 1991 [7], Taylor and Coombes 1993 [8]), в которых метод главных компонент обобщается на моменты более высокого порядка. Эти сети позволяют анализировать данные более сложной природы – приближать их поверхностью, отличающейся от плоскости как в методе главных компонент. Применения метода главных компонент и обобщенного метода главных компонент для анализа данных не всегда оправдано, поскольку не всегда существуют моменты необходимого порядка у анализируемого закона распределения. В тоже время характеристическая функция существует для любого закона распределения [9].
В последнее время большой интерес проявляется к процессам Леви [10], в связи с использованием этих процессов при моделировании в различных приложениях. Поведение процессов Леви полностью описывается параметрическим семейством одномерных законов распределения 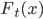 . Семейство законов распределения однозначно определяется семейством характеристических функций:
. Семейство законов распределения однозначно определяется семейством характеристических функций:
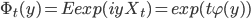 |
(3) |
В (3) характеристическая экспонента
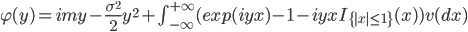 |
(4) |
Несобственный интеграл Лебега в (4) вычисляется по мере Леви, обладающей следующим свойством:
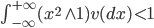 |
(5) |
Интеграл отвечает за скачкообразную составляющую процесса Леви. Приращения процесса Леви 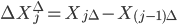 - независимые и одинаково распределенные случайные величины с характеристической функцией
- независимые и одинаково распределенные случайные величины с характеристической функцией 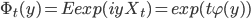 . Положив
. Положив 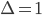 , получим соотношение, которое в дальнейшем будет использовано для оценки характеристической экспоненты. Далее будем использовать обозначение:
, получим соотношение, которое в дальнейшем будет использовано для оценки характеристической экспоненты. Далее будем использовать обозначение: 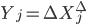 . Как уже отмечалось случайные величины Y - независимые и одинаково распределенные случайные величины. Их общая характеристическая функция может быть представлена следующим образом:
. Как уже отмечалось случайные величины Y - независимые и одинаково распределенные случайные величины. Их общая характеристическая функция может быть представлена следующим образом:
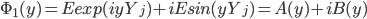 . . |
Отсюда
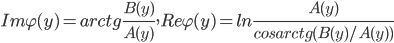 |
(6) |
Формула (6) позволяет вычислить характеристическую экспоненту, используя оценки A и B. Далее рассматривается оценка A(y), поскольку оценка B(y) выполняется аналогично.
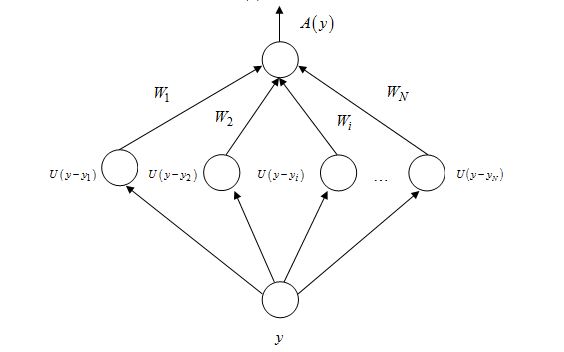
Алгоритм обучения нейросети, использующий потенциальные функции. Структура нейросети, предназначенной для вычисления оценки A(y) представлена на рис. 1.
Рис.1. Структура нейросети (The neural network structure)
Допустим, что нам необходимо вычислять характеристическую экспоненту в интервале значений аргумента: ![[\alpha, \beta]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_449a655262b1fd7ada210efdeeea929f.gif) разобьем данный интервал на N частей с требуемой точностью вычислений. Определим потенциальную функцию U(y) следующими условиями:
разобьем данный интервал на N частей с требуемой точностью вычислений. Определим потенциальную функцию U(y) следующими условиями:
а) носителем функции является симметричный интервал ![[-h, h]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_8d6c91078e70e2eb35a34e153bd86542.gif) ;
;
б) функция является симметричной;
в) функция является гладкой, на интервале ![[-h, 0]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_5870f47875ed7aff453b238f263e4296.gif) функция возрастает, на интервале
функция возрастает, на интервале ![[0, h]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_4f2f500b0ea729a72e799ec122e988b7.gif) функция убывает.
функция убывает.
Примером такой функции может служить функция Ланцоша [11] 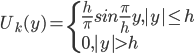 . В качестве критерия обучения рассмотрим средний квадрат отклонения:
. В качестве критерия обучения рассмотрим средний квадрат отклонения:
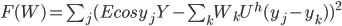 |
(7) |
В (7) закон распределения 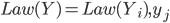 - точки разбиения интервала
- точки разбиения интервала ![[\alpha, \beta]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_449a655262b1fd7ada210efdeeea929f.gif) . Задача обучения заключается в вычислении минимума
. Задача обучения заключается в вычислении минимума 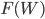 .
.
Наиболее простая ситуация получается если h совпадает с длиной элементарного интервала разбиения - 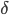 . В этом случае критерий обучения (7) будет иметь вид:
. В этом случае критерий обучения (7) будет иметь вид:
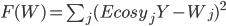 |
(8) |
Из этого соотношения следует, что минимум критерия обучения достигается, когда 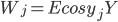 . Следовательно, алгоритм обучения определяется равенствами:
. Следовательно, алгоритм обучения определяется равенствами:
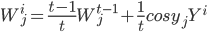 |
(9) |
Для общего случая 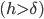 может быть применен стохастический аналог адаптивного алгоритма обучения [12]:
может быть применен стохастический аналог адаптивного алгоритма обучения [12]:
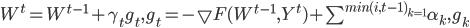 |
(10) |
В формуле (10) 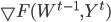 - стохастический градиент критерия
- стохастический градиент критерия 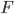 ,
, 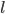 -я координата которого
-я координата которого 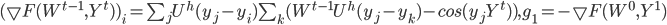 , .
, .
Далее рассматривается пример оценки вещественной части характеристической функции для гиперболического распределения при помощи адаптивного алгоритма обучения.
Гиперболические распределения. В 1997 году О. Барндорфф-Нильсен предложил [13] обобщенные гиперболические распределения. Введение этих распределений обусловлено необходимостью описания некоторых эмпирических закономерностей в геологии, геоморфологии, турбулентности и финансовой математики.
Собственно гиперболическое распределение и гауссовское\\обратно-гауссовское распределение являются наиболее употребительными распределениями. Каждое из этих распределений является смесью нормальных законов:
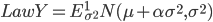 с плотностью с плотностью 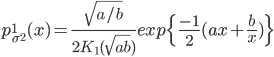 и 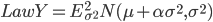 с плотностью с плотностью 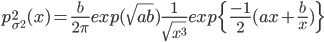 . . |
(11) |
В (11) 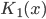 - модифицированная функция Бесселя третьего рода с индексом 1. Остановимся на одном из распределений, например, на гиперболическом распределении. Характеристическая функция, благодаря (11), будет иметь вид:
- модифицированная функция Бесселя третьего рода с индексом 1. Остановимся на одном из распределений, например, на гиперболическом распределении. Характеристическая функция, благодаря (11), будет иметь вид: 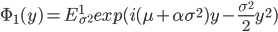 . С использованием соответствующей плотности (11) получим равенство для вещественной части характеристической функции:
. С использованием соответствующей плотности (11) получим равенство для вещественной части характеристической функции:
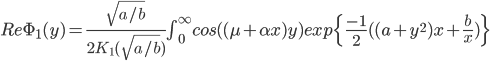 |
(12) |
Формула (12) позволяет вычислить вещественную часть характеристической функции, используя численное интегрирование. Это в свою очередь позволяет определить различие между оценкой, полученной с помощью обучения нейросети, со значением, полученным по формуле (12). Для получения обучающей выборки использовались два генератора. С помощью первого генератора выбиралась дисперсия - 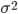 , при этом использовалась первая плотность из (11), затем генерировалась нормальная случайная величина -
, при этом использовалась первая плотность из (11), затем генерировалась нормальная случайная величина - 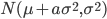 . Результаты расчетов приведены на рис.2. Параметры гиперболического распределения в эксперименте принимали следующие значения:
. Результаты расчетов приведены на рис.2. Параметры гиперболического распределения в эксперименте принимали следующие значения: 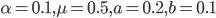 . Число итераций составило 325.
. Число итераций составило 325.
Рис. 2. Вещественная часть характеристической функции гиперболического распределения. Пунктирная линия соответствует численному интегрированию, сплошная линия получена в результате обучения нейросети адаптивным алгоритмом (The real part of the characteristic features of a hyperbolic distribution. The dotted line corresponds to the numerical integration, continuous line obtained as a result of neural network training using a adaptive algorithm).
Таким образом, после обучения нейросеть с удовлетворительной степенью точности позволяет вычислять оценку основной характеристики процесса Леви – характеристической экспоненты.
Замечание. Кроме выше перечисленных работ следует упомянуть работу Dente J. A. [14], в которой излагается идея оценки характеристической функции с помощью обучения нейросети. Основное отличие нашего исследования состоит в использовании другого алгоритма обучения. Кроме этого заметим, что эта методика применима только для процессов с независимыми и однородными приращениями, к которым относятся процессы Леви. В противном случае необходимо учитывать зависимость характеристической функции от времени.
Литература
- Hebb, D. O. Organization of behavior. New York: Wiley, 1949, 335 p.
- Белявский Г.И. О некоторых алгоритмах определения главных компонент в пространстве признаков // Математический анализ и его приложения. Ростов-на-Дону: Изд-во РГУ, 1975. №7. С. 63-67.
- Sanger, T. D. Optimal unsupervised learning in a single-layer linear feedforward neural network // Neural Networks 2, 1989, pp. 459-
- Oja E. Neural networks, principal components and subspaces // J. of Neural Systems, 1989. №1, pp. 61-68.
- Oja E. Principal components, minor components and linear neural networks // Neural Networks, 1992. №5, 927-935.
- Dente J. A. and Vilela Mendes R. // Unsupervised learning in general connectionist systems, Network: Computation in Neural Systems, №7, pp. 123-139.
- Softy, W. R. and Kammen, D. M. Correlations in high dimensional or asymmetric data sets: Hebbian neuronal processing // Neural Networks, 1991. №4, pp. 337-
- Taylor J. G. and Coombes S. Learning higher order correlations, Neural Networks, 1993. №6, pp. 423-
- Lukacs E. Characteristic functions, Griffin’s Statistical Monographs& Courses, No. 5. Hafner Publishing Co., New York, 1960, 216 p.
- Cont R.,Tankov P. Financial modeling with jump processes. London: Chapman Hall / CRC, 2004, 606 p.
- Жуков М.И. Метод Фурье в вычислительной математике. – М.: Наука, 1992. 176 с.
- Белявский Г.И., Пучков Е.В., Лила В.Б. Алгоритм и программная реализация гибридного метода обучения искусственных нейронных сетей // Международный журнал "Программные продукты и системы". Тверь, 2012. №4. С. 96-100.
- Barndorff-Nielsen O.E. Exponentially decreasing distributions for the logarithm of particle size // Proceeding of the Royal Society. London: Ser. A, Math. Phys V.353, 1977, pp. 401
- Joaquim A. Dente, R. Vilela Mendes Characteristic functions and process identification by neural networks // arXiv: physics 9712035 v1[physics.data-an], 1997, pp. 1465
Опубликовано в: Международный журнал "Программные продукты и системы", Тверь, №3, 2015 г.