Методология обучения рекуррентной искусственной нейронной сети с динамической стековой памятью
Авторы статьи: Лила В.Б., Пучков Е.В.
К одному из сложных видов искусственных нейронных сетей (ИНС) относятся рекуррентные, в которых имеются обратные связи. В первых рекуррентных ИНС главной идеей было обучение своему выходному сигналу на предыдущем шаге. Рекуррентные сети реализуют нелинейные модели, которые могут быть применены для оптимального управления процессами, изменяющимися во времени, то есть обратные связи позволяют обеспечить адаптивное запоминание прошлых временных событий. Обобщение рекуррентных ИНС позволит создать более гибкий инструмент для построения нелинейных моделей. Рассмотрим некоторые архитектуры рекуррентных ИНС.
В основе сети Джордана лежит многослойный персептрон. Обратная связь реализуется через подачу на входной слой не только исходных данных, но и сигналов выхода сети с задержкой на один или несколько тактов, что позволяет учесть предысторию наблюдаемых процессов и накопить информацию для выработки правильной стратегии управления [1, 2].
Сеть Элмана так же, как и сеть Джордана получается из многослойного персептрона введением обратных связей. Только сигналы на входной слой идут не от выходов сети, а от выходов нейронов скрытого слоя [1, 2]. Пример архитектуры сети Элмана показан на рис. 1. Выходы скрытого слоя {c1, c2,…,ck} подаются с временной задержкой на входные нейроны с весовыми коэффициентам {wij}-1 , где i – индекс нейрона, на который подается сигнал (i = 1,2,…,n), j – индекс выходного сигнала нейрона скрытого слоя (j = 1,2…,k).
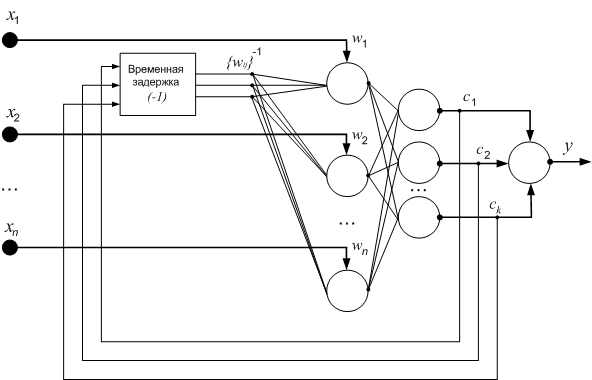 Рис. 1. Пример архитектуры сети Элмана
Рис. 1. Пример архитектуры сети Элмана
Для обобщения рекуррентных ИНС в статье предлагается добавить задержку сигналов обратной связи скрытого слоя на нескольких тактов. Для этого добавим у слоя динамическую стековую память. Пример архитектуры такой ИНС показан на рис. 2.
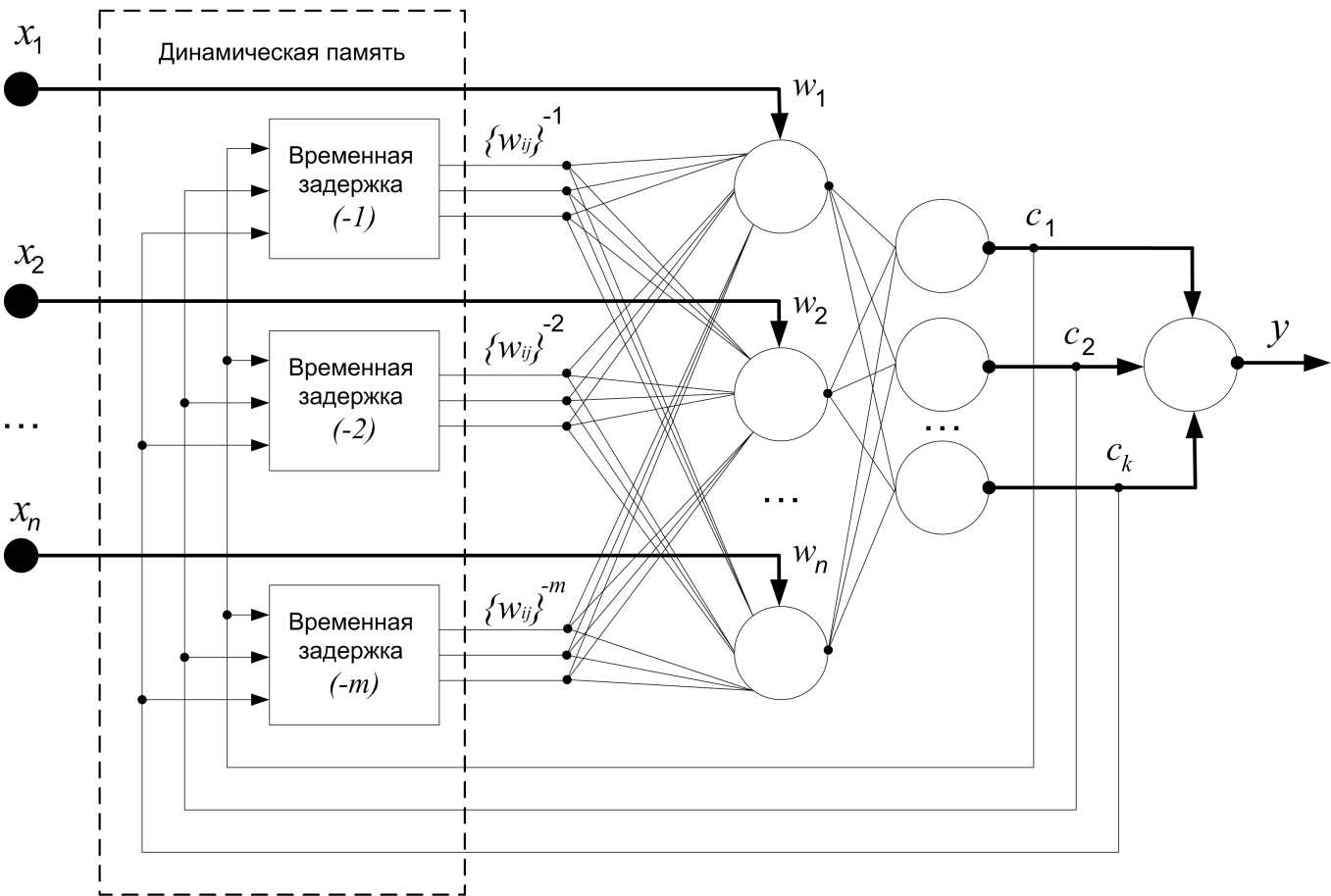 Рис. 2. Пример архитектуры рекуррентной ИНС с динамической стековой памятью нескольких предыдущих выходных сигналов скрытого слоя
Рис. 2. Пример архитектуры рекуррентной ИНС с динамической стековой памятью нескольких предыдущих выходных сигналов скрытого слоя
Выходы скрытого слоя {c1, c2,…,ck} подаются на входные нейроны с весовыми коэффициентам {wij}-t , где i – индекс нейрона, на который подается сигнал (i = 1,2,…,n), j – индекс выходного сигнала нейрона скрытого слоя (j = 1,2…,k), t – индекс временной задержки (t =1,2…m). Количество временных задержек будем изменять от 1 до m. Таким образом, сеть Элмана получается при m=1, а многослойный персептрон – при m=0.
При детальном рассмотрении архитектуры рекуррентной сети видно, что обратные связи от скрытого слоя или от выхода сети можно исключить путем добавления в обучающую выборку сигналов обратной связи.
Рассмотрим процесс трансформации обучающей выборки для решения задачи прогнозирования временного ряда с помощью рекуррентной ИНС с динамической стековой памятью. В качестве примера будем использовать среднемесячные значения плотности потока солнечного излучения на длине волны 10,7 за 2010-2012 года (табл. 1) [3].
Таблица 1. Данные о плотности потока солнечного излучения на длине волны 10,7 см. за 2010-2012 гг
| № примера | Дата | Плотность потока излучения 10-22[Вт/м2] |
| 1 | Январь 2010 | 834,84 |
| 2 | Февраль 2010 | 847,86 |
| 3 | Март 2010 | 833,55 |
| 4 | Апрель 2010 | 759,67 |
| 5 | Май 2010 | 738,71 |
| 6 | Июнь 2010 | 725,67 |
| 7 | Июль 2010 | 799,03 |
| 8 | Август 2010 | 797,10 |
| 9 | Сентябрь 2010 | 811,67 |
| 10 | Октябрь 2010 | 816,77 |
| 11 | Ноябрь 2010 | 824,67 |
| 12 | Декабрь 2010 | 843,23 |
| 13 | Январь 2011 | 837,42 |
| 14 | Февраль 2011 | 945,71 |
| 15 | Март 2011 | 1153,87 |
| 16 | Апрель 2011 | 1130,67 |
| 17 | Май 2011 | 959,68 |
| 18 | Июнь 2011 | 959,33 |
| 19 | Июль 2011 | 942,58 |
| 20 | Август 2011 | 1017,74 |
| 21 | Сентябрь 2011 | 1345,00 |
| 22 | Октябрь 2011 | 1372,90 |
| 23 | Ноябрь 2011 | 1531,67 |
| 24 | Декабрь 2011 | 1413,55 |
| 25 | Январь 2012 | 1330,00 |
| 26 | Февраль 2012 | 1067,93 |
| 27 | Март 2012 | 1151,29 |
| 28 | Апрель 2012 | 1131,67 |
| 29 | Май 2012 | 1215,48 |
| 30 | Июнь 2012 | 1204,00 |
Трансформируем временной ряд методом скользящих окон [4], как показано в таблице 2.
Таблица 2. Обучающая выборка ИНС для решения задачи прогнозирования, полученная в результате преобразования временного ряда методом окон
| № примера | Входы ИНС (x) | Выходы ИНС (y) | ||
| x1 | x2 | x3 | y1 | |
| 1 | 834,84 | 847,86 | 833,55 | 759,67 |
| 2 | 847,86 | 833,55 | 759,67 | 738,71 |
| 3 | 833,55 | 759,67 | 738,71 | 725,67 |
| … | ||||
Пусть в рекуррентной ИНС скрытый слой содержит три нейрона, выходной – один нейрон, стек динамической памяти – обратные сигналы скрытого слоя с задержкой на два такта (рис. 3).
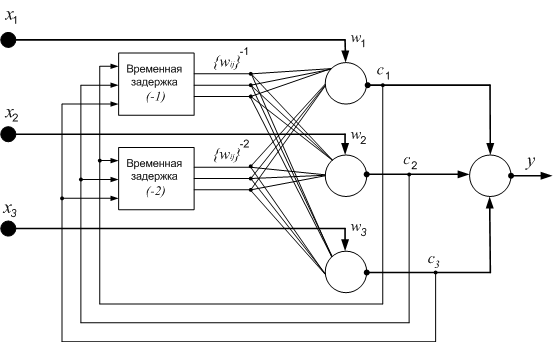 Рис. 3. Рекуррентная ИНС с памятью двух предыдущих выходных сигналов скрытого слоя
Рис. 3. Рекуррентная ИНС с памятью двух предыдущих выходных сигналов скрытого слоя
Так как число нейронов скрытого слоя, имеющих обратную связь с входным слоем, равно трем, то размер входного вектора во время обучения ИНС при запоминании предыдущего выходного сигнала на один шаг назад увеличится на три, при запоминании двух предыдущих выходных сигналов – на шесть. Обозначим входные сигналы обучающей выборки, не изменяющиеся во время трансформации, как {x1, x2, x3}, а сигналы обратной связи – {x4, x5, x6, x7, x8, x9}. В таблице 3 приведена трансформированная обучающая выборка.
Таблица 3. Добавление в обучающую выборку рекуррентной ИНС выходных сигналов скрытого слоя
| № п/п | Входы ИНС (x) | Выходы ИНС (y) | ||||||||
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | y1 | |
| 1 | 834,84 | 847,86 | 833,55 | 0 | 0 | 0 | 0 | 0 | 0 | 759,67 |
| 2 | 847,86 | 833,55 | 759,67 | c1-1 | c2-1 | c3-1 | 0 | 0 | 0 | 738,71 |
| 3 | 833,55 | 759,67 | 738,71 | c1-1 | c2-1 | c3-1 | c1-2 | c2-2 | c3-2 | 725,67 |
| … | ||||||||||
На входы {x4, x5, x6} подаются выходные сигналы скрытого слоя с задержкой на один такт {с1-1,c2-1,c3-1}, на входы {x7, x8, x9} – выходные сигналы скрытого слоя с задержкой на два такта {с1-2,c2-2,c3-2}.
Таким образом, обучение рекуррентной ИНС с динамической стековой памятью методом обратного распространения ошибки можно свести к обучению многослойного персептрона, трансформируя обучающую выборку. Для реализации предлагаемой методологии обучения рекуррентной ИНС с динамической стековой памятью расширены возможности нейроэмулятора NeuroNADS [5].
Объектно-ориентированная модель рекуррентной ИНС с динамической стековой памятью представлена на диаграмме классов (рис. 4).
 Рис. 4. Диаграмма основных классов, реализующих рекуррентную ИНС с динамической стековой памятью
Рис. 4. Диаграмма основных классов, реализующих рекуррентную ИНС с динамической стековой памятью
В отличие от класса Layer, который является контейнером для нейронов многослойного персептрона, класс LayerMemory cодержит память stackOut, реализованную в виде стека предыдущих сигналов слоя. Размер стека задается с помощью свойства stackSize. На схеме (рис. 5) память слоя изображена в виде стека выходных сигналов слоя {y-1, y-2, …, y-n}, где n – размер стека. Каждая ячейка стека y-i состоит из массива выходов нейронов слоя {y1, y2, …, yn}. Стек организован так, что после переполнения памяти последняя ячейка y-n удаляется, вся очередь сдвигается на одну позицию, так что y-i = y-(i-1).
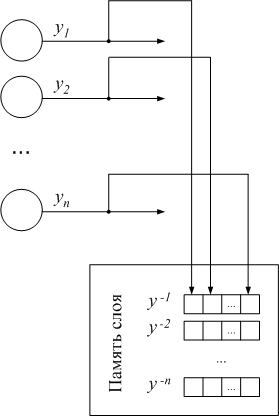 Рис. 5. Реализация слоя с памятью (LayerMemory) для рекуррентных ИНС с динамической стековой памятью
Рис. 5. Реализация слоя с памятью (LayerMemory) для рекуррентных ИНС с динамической стековой памятью
Проведем прогноз среднемесячной плотности солнечной активности на длине волны 10,7 см на первые шесть месяцев 2012 года на основе данных за 2010-2011 года из табл. 1. Для этого построим и обучим рекуррентную ИНС с динамической стековой памятью (рис.3) с помощью нейроэмулятора NeuroNADS. Первые 24 примера временного ряда возьмем для обучающей выборки, а оставшиеся шесть примеров – для тестовой выборки.
Обучение проведем гибридным алгоритмом [6]. Параметры алгоритма: шаг обучения – 0,3, максимальное количество особей в поколении – 10, коэффициент мутации – 0,1. Критерии остановки обучения: среднеквадратическая ошибка – 0,001, количество эпох – 1000.
Один из лучших результатов обучения ИНС представлен на рис. 6 и на рис. 7. Показатели ошибок прогнозирования временного ряда представлены в табл. 4.
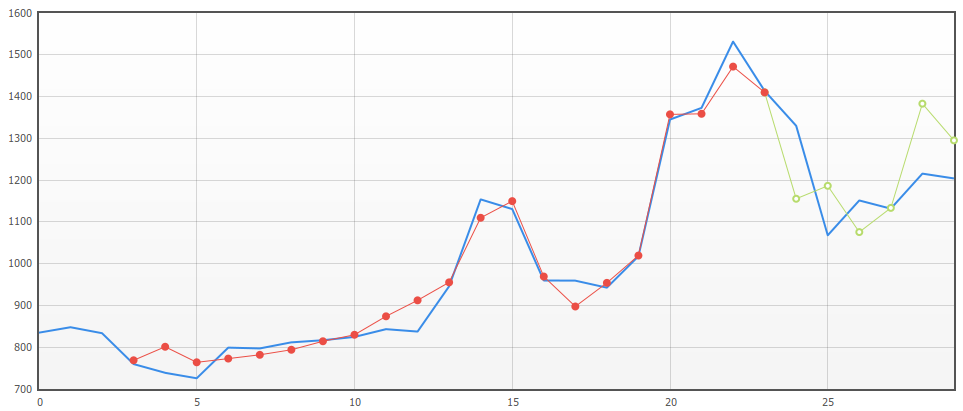 синий график исходного временного ряда;
синий график исходного временного ряда;
красный график выходных значений сети на обучающей выборке;
зеленый график предсказанных значений сети.
Рис. 6. Результаты опроса рекуррентной ИНС с динамической стековой памятью на обучающей и тестовой выборках (по оси абсцисс – номер примера, по оси ординат – значение временного ряда)
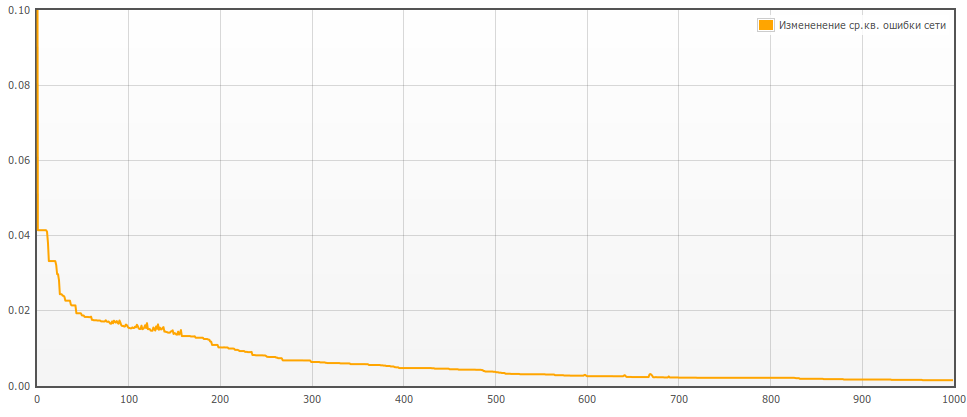 Рис. 7. График изменения функции среднеквадратической ошибки рекуррентной ИНС с динамической стековой памятью во время обучения (по оси абсцисс – количество эпох, по оси ординат – значение ошибки)
Рис. 7. График изменения функции среднеквадратической ошибки рекуррентной ИНС с динамической стековой памятью во время обучения (по оси абсцисс – количество эпох, по оси ординат – значение ошибки)
Таблица 4. Показатели ошибок прогнозирования временного ряда
| Показатели | Значения |
| Среднеквадратическая ошибка (MSE) | 0,00154 |
| Средняя абсолютная ошибка в процентахна обучающей выборке (MAPE) | 2,6% |
| Средняя абсолютная ошибка в процентахна тестовой выборке (MAPE) | 15,5% |
| Средняя абсолютная ошибкана обучающей выборке (MAE) | 25,21 |
| Средняя абсолютная ошибкана тестовой выборке (MAE) | 181,37 |
По результатам обучения можно сделать вывод, что рекуррентная ИНС с динамической стековой памятью справилась с задачей, показатели ошибок прогнозирования временного ряда соответствуют допустимым значениям. Таким образом, рекуррентные ИНС с динамической стековой памятью можно обучать с помощью предложенной методологии, а построенные модели ИНС использовать для прогнозирования временных рядов.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 14-01-00579 а.
Список литературы:
- Бодянский Е.В., Руденко О.Г. Искусственные нейронные сети: архитектуры, обучение, применения. – Харьков: ТЕЛЕТЕХ, 2004. – 369 с.
- Осовский С. Нейронные сети для обработки информации / Пер. с польского И.Д. Рудинского. – М.: Финансы и статистика, 2002. – 344 с.
- Информационно-аналитическая система [Электронный ресурс]: данные о солнечной и геомагнитной активности – Режим доступа: http://moveinfo.ru/data/sun/select (доступ свободный) – Загл. с экрана. – Яз. рус.
- Круг П.Г. Нейронные сети и нейрокомпьютеры. М.: Издательство МЭИ, 2002 г. – 176 с.
- Нейроэмулятор NeuroNADS [Электронный ресурс]: веб-сервис — Режим доступа: http://www.service.i-intellect.ru (ограниченный доступ) – Загл. с экрана. – Яз. рус.
- Белявский Г.И., Пучков Е.В., Лила В.Б. Алгоритм и программная реализация гибридного метода обучения искусственных нейронных сетей // Программные продукты и системы. Тверь, 2012. №4. С. 96 - 100.
Опубликовано в: Международный журнал "Программные продукты и системы", Тверь, №4, 2014 г.


