Сравнительный анализ алгоритмов обучения искусственной нейронной сети

2013/12/04 Статьи

Автор статьи: Е.В. Пучков

Методы обучения искусственных нейронных сетей (ИНС) разделяют на четыре категории: нулевого порядка, первого порядка, второго порядка и нелокальные модификации одноточечных методов. Поскольку целевая функция в задачах обучения многоэкстремальная, для нахождения глобального экстремума используют генетические алгоритмы, методы облака, рестартов, поколений, модифицированный метод многогранника. Более подробно с ними можно ознакомиться в [1, 2, 3, 4].

В основе многих алгоритмов обучения ИНС типа многослойный персептрон лежит итерационный процесс корректировки весовых коэффициентов , для которого необходимо выбрать направление движения и шаг [1]:

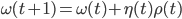\omega(t+1)=\omega(t)+\eta(t)\rho(t)\omega(t+1)=\omega(t)+\eta(t)\rho(t)

где вектор 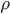\rho\rho – направление движения; 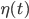\eta(t)\eta(t) – размер шага; t – порядковый номер текущей итерации. Благодаря известному методу обратного распространения ошибки можно произвести декомпозицию сложной задачи обучения.

В статье проводится сравнение алгоритмов обучения ИНС таких, как генетический [5], адаптивный [6] и гибридный [7]. Использованы данные для задачи классификации «Ирисы Фишера» [8], в качестве экспериментальной среды выбрана веб-версия нейроэмулятора NeuroNADS [9, 10]. Построены комитеты размером 10 полносвязных двухслойных нейронных сетей с применением каждого алгоритма. Количество нейронов в скрытом слое – 9 (согласно теореме Колмогорова-Арнольда-Хехт-Нильсена). Критерий остановки обучения ИНС – среднеквадратическая ошибка со значением 0,01, размер шага 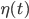\eta(t)\eta(t) – 0,1. Примеры из обучающей выборки подавались случайно. В качестве функций активации нейронов использовались простые сигмоиды.

В последнее время часто решают задачи поиска глобального экстремума с помощью генетических алгоритмов. Обучение ИНС с помощью генетического алгоритма происходит в два этапа. На первом – формируются новые хромосомы, на втором – отбираются наилучшие хромосомы в популяцию. В качестве хромосомы выступают веса нейронов ИНС.

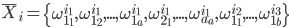\overline X_i = \left\{ \omega_{1_{1}}^{i_1}, \omega_{1_{2}}^{i_1}, ..., \omega_{1_{a}}^{i_1}, \omega_{2_{1}}^{i_1}, ..., \omega_{a_{a}}^{i_1}, \omega_{1_{1}}^{i_2}, ..., \omega_{1_{b}}^{i_3} \right\} \overline X_i = \left\{ \omega_{1_{1}}^{i_1}, \omega_{1_{2}}^{i_1}, ..., \omega_{1_{a}}^{i_1}, \omega_{2_{1}}^{i_1}, ..., \omega_{a_{a}}^{i_1}, \omega_{1_{1}}^{i_2}, ..., \omega_{1_{b}}^{i_3} \right\}

где X – хромосома; i – индекс представителя популяции; 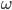\omega\omega – вес нейрона.

Новые хромосомы образуются в результате скрещивания и различных видов мутаций, которые можно проводить в произвольном порядке в пределах одной эпохи. Хромосома, соответствующая заданному критерию качества (в случае с ИНС – это ошибка обучения), будет отобрана в качестве наилучшей.

Результаты применения генетического алгоритма представлены на рис.1.

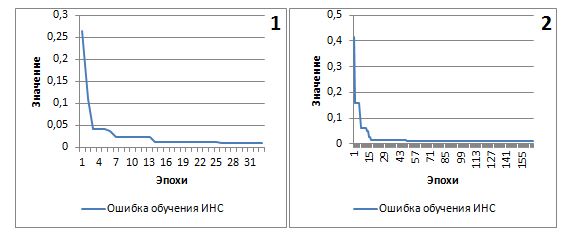grafic_zavisimosti_oshibki_obychenyРис. 1. – График зависимости ошибки обучения от количества эпох для генетического алгоритма (1–лучший, 2–худший результаты)

Генетический алгоритм справился с поставленной задачей, но интенсивность изменения ошибки обучения резко снижалась после 15 эпох. Среднее время обучения ИНС составило 109 эпох.

В методе сопряженных градиентов, который относится к методам обучения первого порядка, формулу поиска минимума на основе предыдущих направлений можно обобщить [5]:

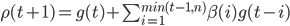\rho(t+1)=g(t)+\sum_{i=1}^{min(t-1,n)}\beta(i)g(t-i)\rho(t+1)=g(t)+\sum_{i=1}^{min(t-1,n)}\beta(i)g(t-i)

где вектор 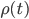\rho(t)\rho(t) – направление движения; 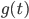g(t)g(t)– направление антиградиента на текущей итерации tt; 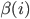\beta(i)\beta(i) - коэффициент, определяющий вес 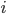ii -го градиента; 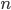nn – количество запоминаемых градиентов. При 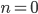n = 0n = 0 получим простой градиентный спуск, а при n = \inftyn = \infty, суммируя все предыдущие направления – методы сопряженных градиентов. Настройка параметра 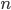nn и последовательностей 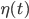\eta(t)\eta(t), из формул (1) и (2), соответственно, позволит использовать более гибкое решение – адаптивный алгоритм обучения ИНС [5].

На рис. 2 представлены графики зависимости ошибки обучения от количества эпох для адаптивного алгоритма.

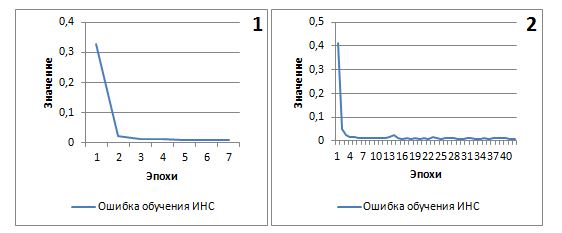grafic_zavis_dlya_adapt_algorРис. 2. – График зависимости ошибки обучения от количества эпох для адаптивного алгоритма (1–лучший, 2–худший результаты)

Среднее время обучения ИНС с применением адаптивного алгоритма составило 22 эпохи, что в 5 раз меньше, чем среднее время обучения генетическим алгоритмом. Сходимость алгоритма к локальному минимуму наступала за 5-7 эпох.

Последний метод, который мы будем использовать для обучения ИНС, основан на последовательном применении адаптивного и генетического алгоритмов [6]. Отметим, что при переходе к генетическому алгоритму добавляется к популяции хромосома – ИНС, обученная адаптивным алгоритмом. В качестве критерия перехода используется значение ошибки обучения равное 0,015. На рис. 3 изображены графики зависимости ошибки обучения от количества эпох для гибридного метода.

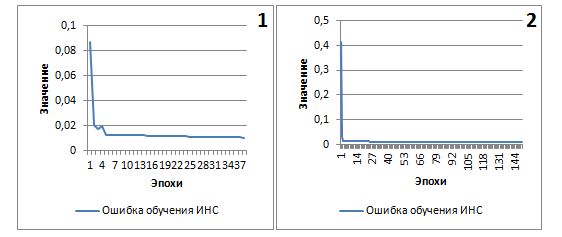grafic_zavis_dlya_gibridn_metРис. 3. – График зависимости ошибки обучения от количества эпох для гибридного метода (1–лучший, 2–худший результаты)

По результатам сравнения адаптивный алгоритм сходится быстрее, чем генетический и гибридный (таблица №1). Окончательный выбор алгоритма будет зависеть от конкретный задачи, потому что в задаче со сложной целевой многоэкстремальной функцией, в которой с помощью гибридного алгоритма можно быстрее вычислить решение в окрестности глобального минимума, адаптивный алгоритм может показать результаты хуже [7].

Отметим, что данные результаты не могут в полной мере определять точность классификации и точность метода, поскольку не проводилась оценка количества распознанных экземпляров ириса и не исследовалась обобщающая способность построенных ИНС.

Таблица №1. Время обучения ИНС (эпохи)

Номер ИНС

Алгоритм

 Гибридный метод
генетический адаптивный
1 32 20 38
2 54 21 86
3 70 16 71
4 130 13 35
5 101 35 96
6 156 20 131
7 80 12 52
8 168 41 148
9 136 38 37
10 164 6 103
Среднее 109 22 80

 

Список литературы:

  1. Хайкин С. Нейронные сети: полный курс, 2-е изд.; – пер. с англ/ С. Хайкин. – М.: Издательский дом «Вильямс», 2006. – 1104 с.
  2. Тархов Д.А. Нейронные сети. Модели и алгоритмы. Кн.18: справочное издание. (Серия "Нейрокомпьютеры и их применение"). – М. : Радиотехника, 2005. – 256 с.
  3. Бодянский Е.В., Руденко О.Г. Искусственные нейронные сети: архитектуры, обучение, применения. – Харьков: ТЕЛЕТЕХ, 2004. – 369 с.
  4. Осовский С. Нейронные сети для обработки информации / Пер. с польского И.Д. Рудинского. – М.: Финансы и статистика, 2002. – 344 с.
  5. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы; пер. с польск. И. Д. Рудинского. – М.: Горячая линия -Телеком, 2006. – 452 c.
  6. Лила В.Б. Алгоритм и программная реализация адаптивного метода обучения искусственных нейронных сетей [Электронный ресурс] // Инженерный вестник Дона, 2012, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/626 (доступ свободный) – Загл. с экрана. – Яз. рус.
  7. Белявский Г.И., Пучков Е.В., Лила В.Б. Алгоритм и программная реализация гибридного метода обучения искусственных нейронных сетей // Программные продукты и системы. – Тверь, 2012. – №4. – с. 96 - 100.
  8. Iris Data Set. The UCI Machine Learning Repository  [Электронный ресурс]. – Режим доступа: http://archive.ics.uci.edu/ml/datasets/Iris (доступ свободный) – Загл. с экрана. – Яз. англ.
  9. Пучков Е.В. Применение нейроэмулятора «NeuroNADS» для определения ступени и времени торможения при управлении горочными замедлителями [Электронный ресурс] // Инженерный вестник Дона, 2010, №4. – Режим доступа: http://ivdon.ru/magazine/latest/n4y2010/263 (доступ свободный) – Загл. с экрана. – Яз. рус.
  10. NeuroNADS [Электронный ресурс]: веб-сервис — Режим доступа: http://www.service.i-intellect.ru/emulator.php (ограниченный доступ) – Загл. с экрана. – Яз. рус.

 

Опубликовано в: Научно-инновационный журнал «Инженерный вестник Дона»: №4, Ростов н/Д: 2013.