Прогнозирование социально-экономических показателей с помощью многомерных динамических моделей временных рядов

2017/11/30 Статьи

Автор статьи: В.В. Мисюра

Целью представленной работы является рассмотрение и изучение методов прогнозирования временных рядов на основе многомерного подхода на примере исследования социально-экономических показателей. Вопросам прогнозирования временных рядов уделяется значительное внимание в литературе, начиная с учебников по математической статистике и эконометрике и заканчивая узкоспециализированными научными журналами. В представленной работе будем опираться на математический аппарат,  предложенный в источниках [1, 2, 3, 4, 5, 6, 7].

Для решения задач прогнозирования достаточно часто применяется статистический аппарат корреляционного-регрессионного анализа, который строится на предыдущих значениях временного ряда. Это обстоятельство не позволяет устанавливать причинно-следственные связи системы социально-экономических показателей в целом. Очевидно, для повышения качества прогноза необходимо проводить одновременный анализ сразу нескольких доступных показателей. Качество прогнозирования временных рядов может быть существенно увеличено использованием многомерного подхода, при котором в прогнозе учитываются не только предшествующие значения уровней временного ряда, но и связь с другими  временными рядами.

В докладе будет рассмотрена задача прогнозирования динамики средней заработной платы РФ (Y) в зависимости от динамики инвестиций в основной капитал (X). Исходные данные для выполнения работы получены на сайте Министерства финансов Российской федерации за период с января 2010 года по октябрь 2015 года. Разобьем выборку на обучающую и контрольную. Прогноз по построенной модели будем сравнивать с контрольной выборкой.

Прежде чем перейти к  прогнозированию временных рядов с учетом их взаимосвязи, необходимо выполнить  анализ каждого временного ряда в отдельности. Предположим, что рассматриваемые временные ряды имеют аддитивную модель (1).

\begin{equation}
Y_t = T_t+S_t + E_t
\end{equation}

где 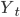Y_t – значение временного ряда в момент t, 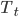T_t – тренд, выбираемый из параметрического семейства,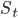S_t – сезонная компонента, 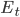E_t – случайная компонента.

Применение критерия «восходящих и нисходящих» серий для проверки гипотезы о существовании тренда (см.[5]) позволило утверждать, что анализируемые временные ряды не содержат трендовую составляющую.

В качестве модели сезонной составляющей будем использовать ряд Фурье:

 

\begin{equation}S_t = a_0 + \sum_{i=1}^k a_i cos (it)+b_i sin(it)
\end{equation}

Значения t – это номера временных периодов (месяц). Для введения в формулу их преобразуют в радиальную меру по формуле: 2p(t–1)/n. Значение n представляет собой количество временных интервалов, например, для года (при помесячном анализе) n = 12, рассчитывают не более четырех гармоник и затем уже определяют, количество гармоник, наилучшим образом отражающих периодичность изменения уровней ряда.

Параметры (2) находим с помощью метода наименьших квадратов.

\begin{equation}\sum_{} (S_t - \hat S_t)^2 \rightarrow min
\end{equation}

Получим:

\begin{equation}
a_0 = \frac{1}{n} \sum_{i=1}^n y_i; a_k = \frac{2}{n} \sum_{i=1}^n y_i cos(kt_i); b_k = \frac{2}{n} \sum_{i=1}^n y_i sin(kt_i)
\end{equation}

В качестве характеристики качества модели будем использовать MAPE – ошибку (Mean PercentageError) [4]:

\begin{equation}
\bar{\gamma} = \frac{1}{l} \sum_{k=1}^l \frac{|Y_k - \hat Y_k|}{Y_k} 100 %
\end{equation}

где 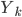Y_k – фактическое значение показателя на k-ое наблюдение; \hat Y_k – прогнозное значение показателя на k-ое наблюдение, l – период прогнозирования.

MAPE – ошибки найденные для моделей с числом гармоник от одной до четырех по формуле (5) представлены в таблице 1.

Таблица 1 – MAPE – ошибки найденные для моделей сезонной составляющей динамики заработной платы с числом гармоник от одной до четырех

Число гармоник K=1 K=2 K=3 K=4
MAPE – ошибки 5,6% 5,5% 4,9% 4,4%

Модель, содержащая четыре гармоники, наилучшим образом отражает периодичность изменения уровней временных рядов (см.рис.1).

Модель оценки периодической составляющей для 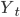Y_t записывается следующим образом

\begin{eqnarray*}
& \hat S_t^Y = 102,1-2,5cos(t)+1,7sin(t)-2,8cos(2t)-3sin(2t)-4cos(3t)-3,3sin(3t)- & \\
& -2,2cos(4t)-3,3sin(4t)
\end{eqnarray*}

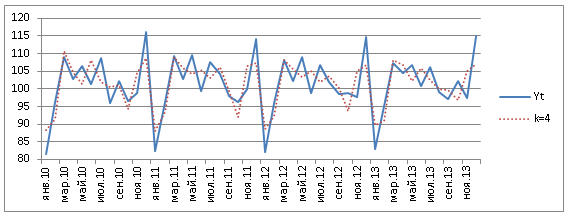
Рисунок 1 – Графики уровней временного ряда динамики Y и
оценки сезонной составляющей Y, содержащей четыре гармоники

Далее будем рассматривать поведение показателя 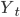Y_t в зависимости от его значения в предшествующий период 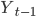Y_{t-1} и значения объясняющей лаговой переменной 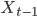X_{t-1}. Т.е., если в некоторый момент времени t происходит изменение X, то это изменение будет влиять на значение Y через l последующих моментов времени.

Математическая модель имеет вид

\begin{eqnarray}
Y_t = \alpha + \beta X_{t-1} + \gamma Y_{t-1} + \varepsilon_t
\end{eqnarray}

Для дальнейшего исследования необходимо предварительно исключить тенденцию и сезонность из анализируемых рядов и перейти к модели

\begin{eqnarray}
\tilde{Y_t} = \alpha + \beta \tilde{X}_{t-1} + \gamma \tilde{Y}_{t-1} + \varepsilon_t
\end{eqnarray}

где \begin{eqnarray} \tilde{Y_t}=Y_t-T_t^Y-S_t^Y+\varepsilon_t^Y , X_t=X_t-T_t^X-S_t^X+\varepsilon_t^X\end{eqnarray}

Далее следует изучить вопрос корреляции временных рядов. Корреляционная связь между уровнями двух динамических рядов называется кросс-корреляцией [5]. На основании рассчитанных коэффициентов кросс-корреляции определяется лаг менее существенной взаимосвязи между динамическими рядами, то есть тот лаг, которому соответствует минимальный по модулю коэффициент кросс-корреляции.

Т.о. модель взаимосвязи временных рядов получила вид:

\begin{eqnarray}
\tilde{Y_t} = \alpha + \beta \tilde{X}_{t-3} + \gamma \tilde{Y}_{t-1} + \varepsilon_t
\end{eqnarray}

Из уравнения (8) следует, что на текущий уровень индекса изменения средней заработной платы РФ оказывает влияние его значение в предыдущий период и индекс инвестиций в основные фонды за соответствующий месяц предыдущего квартала.

Для оценки параметров модели (8) применим стандартные методы регрессионного анализа. Модель (8) принимает вид \begin{eqnarray}
\tilde{Y_t} = 0,0061 - 0999\tilde{Y}{t-1} + 0.082\tilde{X}_{t-3} \end{eqnarray}Построенное уравнение регрессии обладает достаточно хорошим качеством Факторы 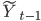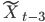\tilde{Y}_{t-1}, \tilde{X}_{t-3} примерно на 85% объясняют вариацию фактора 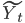\tilde{Y_t} функция регрессии статистически значима, т.е. адекватно описывает исходные данные.

Построенные модели без труда позволяют сделать прогноз динамики заработной платы РФ. Краткосрочное прогнозирование временного ряда 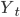Y_t с помощью учета только периодической составляющей в данном исследовании дало неплохие результаты (ошибка 3,9%), но качество прогноза все же улучшилось благодаря использованию динамической модели с лаговыми переменными. Ошибка оказалась равной 1,26%.

Литература

  1. Айвазян С.А. Прикладная статистика. Основы эконометрики / С.А. Айвазян – М.: ЮНИТИ-ДАНА, 2001. – 432 с.
  2. Айвазян С.А. Прикладная статистика: Теория вероятностей и прикладная статистика / С.А. Айвазян, В.С. Мхитарян – М.: ЮНИТИ-ДАНА, 2001. – 656 с.
  3. Афанасьев В.Н. Анализ временных рядов и прогнозирование / В.Н. Афанасьев, М.М. Юзбашев – М.: Финансы и статистика, 2001. – 227 с.
  4. Бородич С.А. Эконометрика / С.А. Бородич– Минск: Новое знание. 2001.–408 с.
  5. Дуброва Т.А. Статистические методы прогнозирования / Т.А. Дуброва – М.: ЮНИТИ-ДАНА, 2003. – 206 с.
  6. Четыркин Е.М. Статистические методы прогнозирования / Е.М. Четыркин – М.: Статистика, 1977. – 192 с.
  7. Эконометрика /Под ред. И.И.Елисеевой.– М.: Финансы и статистика, 2005.– 575 с.
  8. Экономико-математические методы и прикладные модели /Под ред. В.В.Федосеева. – М.: ЮНИТИ-ДАНА, 2005. – 304 с.