Нейросетевое имитационное моделирование скачкообразных процессов на примере устойчивых и умеренно устойчивых процессов
Авторы статьи: Белявский Г.И., Кондратьева Т.Н., Мисюра В.В.
Введение. Процессы Леви можно рассматривать как непрерывный аналог случайного блуждания. Это процессы с траекториями непрерывными справа и имеющими пределы слева. Разрывы траекторий происходят в случайные моменты времени, число которых конечное на любом конечном временном интервале и не более чем счетное на бесконечном интервале. Важное место в теории процессов Леви занимают устойчивые и умеренно устойчивые процессы. Несмотря на то, что основные результаты теории были получены в 30-х годах прошлого столетия, интерес к процессам Леви не ослабевает, в связи с многочисленными приложениями. Например, в таких различных областях, как стохастическая финансовая математика и квантовая теория поля. Следует также отметить, что исследователи постоянно получают новые теоретические и прикладные результаты в области моделирования с использованием процессов Леви. Наиболее полное изложение теории процессов Леви представлено в относительно недавних работах Bertoin [1], Sato [2], в библии по устойчивым процессам Samorodnitsky and Taqqu [3] . Аналитические свойства процессов Леви изложены в работах Jacob [4,5], разнообразные приложения процессов Леви можно найти в работах O. E. Barndorff-Nielsen, T. Mikosch, S. Resnick [6] и работах B. Oksendal, A. Sulem [8].
При применении метода Монте-Карло возникает необходимость в имитационных моделях процессов Леви. Моделированию процессов Леви посвящен раздел в монографии R. Cont, P. Tankov [7].
В статье рассматривается задача моделирования случайных процессов с симметричной мерой Леви при помощи нейросети с обратной связью. При этом используются дискретные симметричные случайные величины, получающиеся в результате вычитания пуассоновских случайных величин. В статье используются результаты работы Белявского Г. и Никоненко Н. [8]. В связи с использованием нейро-сети при моделировании случайных процессов упомянем статью Dente A. [9], посвященную вычислению характеристической функции случайной величины при помощи обучения нейросети.
Модель процесса Леви с ограниченной вариацией на решетке. Рассмотрим полный стохастический базис 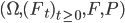 , относительно которого процесс является процессом Леви. Мы будем рассматривать процессы Леви с траекториями ограниченной вариации. Характеристическая экспонента таких процессов имеет вид:
, относительно которого процесс является процессом Леви. Мы будем рассматривать процессы Леви с траекториями ограниченной вариации. Характеристическая экспонента таких процессов имеет вид:
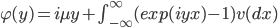 |
(1) |
В (1) мера Леви - 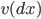 удовлетворяет условию:
удовлетворяет условию:
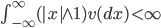 |
(2) |
Рассмотрим значения процесса Леви в узлах решетки на 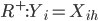 . Последовательность
. Последовательность 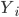 удовлетворяет очевидному рекуррентному уравнению:
удовлетворяет очевидному рекуррентному уравнению: 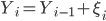 , в котором начальное значение
, в котором начальное значение 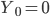 , случайные величины
, случайные величины 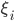 - независимые, одинаково распределенные и безгранично-делимые случайные величины с общей характеристической функцией:
- независимые, одинаково распределенные и безгранично-делимые случайные величины с общей характеристической функцией: 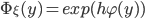 . Определим интервал
. Определим интервал ![[a,b] \subseteq [-1,1]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_b2cd5325f43455b067f88b95c98e809e.gif) и
и 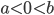 . Оценим абсолютную величину разности
. Оценим абсолютную величину разности 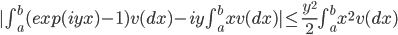 . Выберем наибольшее
. Выберем наибольшее 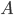 и наименьшее
и наименьшее 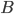 , удовлетворяющие неравенству:
, удовлетворяющие неравенству:
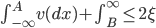 |
(3) |
Определим разбиение 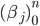 интервала
интервала ![[A, a]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_996d10a1b3d2c02b2ed2368f17de9525.gif) следующим образом:
следующим образом: 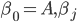 определяется рекуррентным уравнением:
определяется рекуррентным уравнением: 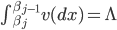 , причем
, причем 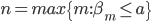 . Аналогично определяется разбиение
. Аналогично определяется разбиение 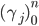 интервала
интервала ![[b, B]](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_beb22ec342c850c76a5777e7498b8bb0.gif) . Рассмотрим приближение для интеграла
. Рассмотрим приближение для интеграла 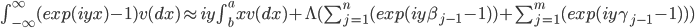 . Погрешность такого приближения
. Погрешность такого приближения 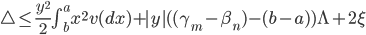 . Таким образом, приближенное представление случайной
. Таким образом, приближенное представление случайной 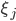 имеет следующий вид:
имеет следующий вид: 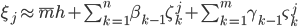 , семейство
, семейство 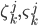 - семейство независимых и одинаково распределенных пуассоновских случайных величин с общей интенсивностью
- семейство независимых и одинаково распределенных пуассоновских случайных величин с общей интенсивностью 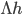 . Это следует из того, что выражение
. Это следует из того, что выражение 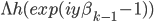 является характеристической функцией для случайной величины:
является характеристической функцией для случайной величины: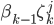 . Константа в этом приближении
. Константа в этом приближении 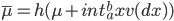 .
.
Рассмотрим случай симметричной меры Леви, то есть 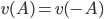 . Для симметричного случая очевидны следующие равенства:
. Для симметричного случая очевидны следующие равенства:
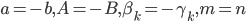 |
(4) |
Из (4) следует приближенное представление случайной величины 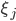 :
: 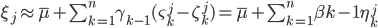 . Симметричный закон распределения разности
. Симметричный закон распределения разности 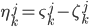 представляется быстро сходящимся рядом:
представляется быстро сходящимся рядом:
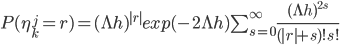 |
(5) |
Оценка погрешности приближенного представления характеристической экспоненты будет иметь вид: 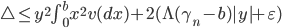 .
.
Структура сети, вычисляющей процесс, представлена на рис.1.
 Рис.1. Нейросетевая модель процесса Леви
Рис.1. Нейросетевая модель процесса Леви
Начальное состояние выходного нейрона равно нулю, случайные величины 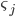 независимые и одинаково распределенные по симметричному закону распределения (5). Обратная связь имеет один такт задержки.
независимые и одинаково распределенные по симметричному закону распределения (5). Обратная связь имеет один такт задержки.
Устойчивый, симметричный процесс Леви. Устойчивые процессы Леви широко распространены как средство моделирования, например, финансовых индексов и трафика. Мера Леви устойчивого симметричного процесса имеет следующий вид:
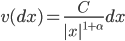 |
(6) |
В (6) 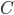 - положительная константа, индекс устойчивости
- положительная константа, индекс устойчивости 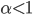 . Последнее неравенство означает, что вариация ограничена почти всюду. Расчетные формулы для параметров нейросетевой модели будут иметь вид:
. Последнее неравенство означает, что вариация ограничена почти всюду. Расчетные формулы для параметров нейросетевой модели будут иметь вид:
![B = (\frac {C}{\alpha \varepsilon})^{1/ \alpha} , \gamma_j = [(\frac{C}{\alpha \gamma^{\alpha}_{j-1}} - \Lambda) \frac{\alpha}{C}]^{\frac{-1}{\alpha}}](http://i-intellect.ru/wp-content/plugins/latex/cache/tex_46bf92723a71e0f1eabc1dd877f4a0e2.gif) |
(7) |
Очевидно, что 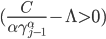 , для всех
, для всех 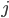 . Отсюда следует, что
. Отсюда следует, что 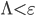 . Положим
. Положим 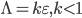 , и рассмотрим неравенство для оценки погрешности
, и рассмотрим неравенство для оценки погрешности 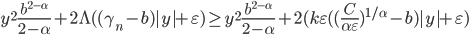 . Таким образом, оценка погрешности при
. Таким образом, оценка погрешности при 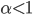 , стремится к бесконечности при
, стремится к бесконечности при 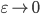 , что делает нейросеть, рассматриваемой архитектуры, неприемлемой для моделирования устойчивого процесса Леви с индексом устойчивости меньшим единицы.
, что делает нейросеть, рассматриваемой архитектуры, неприемлемой для моделирования устойчивого процесса Леви с индексом устойчивости меньшим единицы.
Умеренно устойчивый, симметричный процесс Леви. Мера Леви для данного процесса выглядит следующим образом:
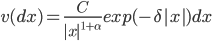 |
(8) |
При 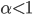 соответствующий процесс Леви – процесс ограниченной вариации.
соответствующий процесс Леви – процесс ограниченной вариации.
Скачки умеренно устойчивого процесса в окрестности нуля ведут себя как скачки устойчивого процесса. Большие скачки процесса за счет множителя 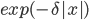 ведут себя умеренно. Умеренно устойчивые процессы особенно популярны при моделировании поведения финансовых индексов [10]. Формулы для вычисления параметров для нейросети будут иметь следующий вид:
ведут себя умеренно. Умеренно устойчивые процессы особенно популярны при моделировании поведения финансовых индексов [10]. Формулы для вычисления параметров для нейросети будут иметь следующий вид:
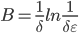 |
(9) |
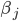 является решением уравнения:
является решением уравнения:
 |
(10) |
Положив 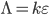 и
и 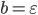 , получим оценку погрешности:
, получим оценку погрешности: 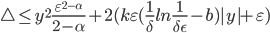 , которая стремится к нулю при
, которая стремится к нулю при 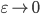 . Это означает, что предлагаемая архитектура нейросети вполне приемлема для моделирования данного процесса Леви. Одна из траекторий такого процесса представлена на рис. 2.
. Это означает, что предлагаемая архитектура нейросети вполне приемлема для моделирования данного процесса Леви. Одна из траекторий такого процесса представлена на рис. 2.
 Рис.2. Траектория умеренно стабильного процесса с параметрами
Рис.2. Траектория умеренно стабильного процесса с параметрами 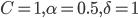 .
.
Заключение. Эффективность предложенной архитектуры нейронной сети заключается в том, что состояния входных нейронов – независимые и одинаково распределенные случайные величины. Этот результат получается в результате неравномерного разбиения фазовой шкалы. Однако, не для всех процессов такая техника применима. В статье приводится пример такого процесса.
Литература
- Bertoin Jean. Lévy processes. Cambridge Tracts in Mathematics, 121. Cambridge University Press.Cambridge, 265 p.
- Sato Ken-iti. Lévy processes and infinitely divisible distributions. Cambridge Studies in Advanced Mathematics, 68. Cambridge University Press, Cambridge, 1999. 486 p.
- Samorodnitsky Gennady, Taqqu Murad S. Stable non-Gaussian random processes. Stochastic models with infinite variance. Stochastic Modeling. Chapman & Hall, New York, 1994. 632 p
- Jacob N. Pseudo-differential operators and Markov processes. Akademie-Verlag, Berlin, 1996. 475 р.
- Jacob N. Pseudo-Differential Operators and Markov Processes. World Scientific, 2001. 516 p.
- Barndorff-Nielsen O. E., Mikosch TResnick (eds.) S. Lévy Processes – Theory and Applications. Birkhauser. Boston, 2001. 401 р.
- Cont R., Tankov P., Financial modelling and jump processes. Chapman & Hall/CRC Financial Mathematics Series, USA, 2004. 533 p.
- Белявский Г., Никоненко Н. Алгоритм расчета безарбитражной цены финансового обязательства на основе дискретизации процессов Леви. // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Информатика. Телекоммуникации. Управление. 2012. Т. 3. № 150. С. 56-59.
- Belyavskii G., Nikonenko N. Algoritm rascheta bezarbitrazhnoi tseny finansovogo obyazatel'stva na osnove diskretizatsii protsessov Levi. [The algorithm for calculating arbitrage-free price of financial liabilities based on the Levi processes sampling.] // Nauchno-tekhnicheskie vedomosti Sankt-Peterburgskogo gosudarstvennogo politekhnicheskogo universiteta. Informatika. Telekommunikatsii. Upravlenie. 2012. T. 3. № 150. pp . 56-59.
- Dente A. Characteristic functions and process identification by neural networks// Neural Networks. Vol.10, No. 8, 1997. pp. 1465-1471.
- Ширяев А.Н. Основы стохастической финансовой математики, т.1. М.: Фазис, 2004. 512 с.
- Shiryaev A.N. Osnovy stokhasticheskoi finansovoi matematiki [Essentials of Stochastic Financial Mathematics], t.1. M.: Fazis, 2004. 512 p.


