Разработка методов динамического построения искусственной нейронной сети на основе ряда Вольтерра и вейвлет-ядра

2015/09/25 Статьи

Авторы статьи: Пучков Е.В., Белявский Г.И.

Введение
Искусственные нейронные сети (ИНС) персептронного типа используются в различных приложениях с большим успехом благодаря тому, что они универсальны и способны к обобщению. Но с другой стороны использование ИНС связано с определенными проблемами, самое главное – нет гарантий, что фиксированная модель будет хорошо работать для решения прикладной задачи. Для получения хорошей точности приближения в центре внимания исследователей были такие аспекты как сбор данных для обучения, пред/постобработка, функции активации нейронов различных видов, инициализация весов в алгоритмах обучения, сами алгоритмы обучения и функции ошибок. Но одним из самых важных этапов моделирования ИНС является построение архитектуры, непосредственно связанной с возможностью модели. Данная статья посвящена архитектуре ИНС. Архитектуру ИНС составляют три элемента:

  • число слоев;
  • число нейронов в каждом слое;
  • функция активации каждого слоя.

 

Уверенно можно определить только входной и выходной слои на основе параметров решаемой прикладной задачи. Таким образом, основная цель состоит в нахождении количества скрытых слоев и числа нейронов в каждом скрытом слое.
Математическое обоснование использования многослойного персептрона восходит к тринадцатой проблеме Гильберта [1] и содержится в:

  1. Теореме Колмогорова-Арнольда [2, 3, 4] о возможности представления любой непрерывной функции многих переменных, которая в терминах ИНС сформулирована Р. Хехт-Нильсеном [5].
  2. Теореме Стоуна-Вейерштрасса [6] об аппроксимации функции многих переменных с помощью функций меньшего числа переменных, которая в терминах ИНС сформулирована В.Я. Крейновичем [7] и в последующем А.Н. Горбанем [8].

 

Использование первой теоремы на практике затруднено тем, что отсутствует конструктивный способ подбора функций активаций нейронов выходного слоя и характеристик сигмоидальных функций активации нейронов скрытого слоя.
Более удачный вариант -это использовать теорему Стоуна-Вейерштраса и теорию вейвлет базиса. Нелинейность функций активации, размер и структура ИНС могут быть произвольными, поэтому существуют только методы получения субоптимального решения [9].
В статье авторы предлагают методы динамического построения ИНС на основе ряда Вольтерра [10] и вейвлет-ядра [11]. Данная работа состоит из двух частей. В этой статье авторы дают теоретическое обоснование предлагаемых методов, предполагая, что следующая работа будет посвящена исключительно экспериментальным результатам и их анализу.

Метод динамического построения ИНС на основе ряда Вольтерра
ИНС Вольтерра - это динамическая сеть c полиномиальной нелинейностью, позволяющая строить модели для идентификации нелинейных объектов, устранения интерференционных шумов, а также прогнозировании переменных во времени нестационарных сигналов, например, прогнозировании транспортных потоков [10, 12]. Разложение Вольтерра для реализации ИНС можно представить в следующей форме:

\widehat{y} = \sum_{i=0}^L x_{t-1} [w_i + \sum_{j=0}^L x_{t-j} [w_ij + \sum_{k=0}^L x_{t-k(w_ijk+...)}]]

Каждое слагаемое в квадратных кнопках скобках представляет собой линейный фильтр первого порядка (КИХ-фильтр), где соответствующие веса представляют импульсную реакцию другого линейного фильтра следующего уровня. Приняты следующие обозначения:
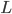X = [x_t, x_{t-1}, ..., x_{t-L}]^T - входной вектор, L -количество единичных задержек, 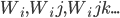W_i, W_ij, W_ijk ... - веса ИНС, называемые ядрами Вольтерра, соответствующие реакциям высших порядков, 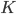K - количество уровней.
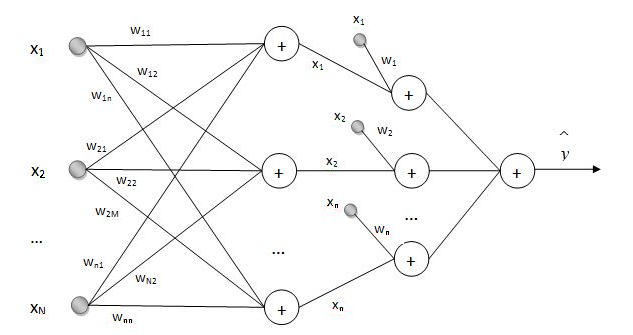
Обучение ИНС Вольтерра, представленной на рисунке 1, предлагается проводить с помощью стохастического аналога адаптивного алгоритма обучения [13], в основе которого заложена идея методов сопряженных градиентов. Подробно об алгоритмах обучения ИНС Вольтерра можно ознакомиться в [10, 12, 14].

structura_ins_volterra

Рис.1. Структура ИНС на основе ряда Вольтерра. Количество уровней K равно 2.

Рассмотрим процесс динамического построения ИНС Вольтерра.
Шаг №1. Определим количество входных нейронов на основе входного вектора X, количество уровней К, на которых создаются фильтры определим равным 1.
Шаг №2. Проведем предварительную нормализацию данных по формуле:

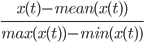
\frac{x(t)-mean(x(t))}{max(x(t))-min(x(t))}

Шаг №3. Инициализируем веса ИНС с помощью нормального распределения или методики Nguyen и Widrow [15].
Шаг №4. Рассчитаем функцию ошибки обучения по формуле:

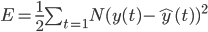
E = \frac{1}{2} \sum_{t=1}{N} (y(t) - \widehat{y} (t))^2

Установим максимальную ошибку 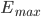E_{max}, если 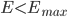E< E_{max} запоминаем значения весов 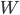W, иначе переходим к шагу 5.
Шаг 5. Используем адаптивный алгоритм обучения [14].
Шаг 6. Оцениваем сложность сети. Считаем, что сложность текущей сети не соответствует поставленной задаче, если ошибка 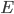E с числом эпох обучения уменьшается недостаточно быстро, либо не уменьшается совсем. Уменьшение скорости ниже заданного порога служит сигналом к тому, что для улучшения результатов при падении скорости ошибки необходимо добавить еще один уровень – очередное слагаемое в ряде Вольтерра. Формально скорость изменения ошибки можно определить следующим образом:

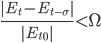
\frac{|E_t - E_{t-\sigma}|}{|E_{t_0}|} < \Omega

Здесь 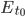E_{t_0} – значение ошибки в момент 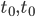t_0, t_0 – момент добавления предыдущего уровня, 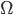\Omega – некоторая заданная минимальная скорость изменения ошибки, при превышении которой принимается решение об изменении сети, 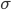\sigma – количество эпох – циклов обучения сети перед про- изведением оценки скорости ошибки.
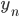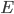Шаг 7. Рассчитываем y_n и E, повторяя обучение до тех пор пока ошибка 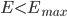E<E_{max}. Запоминаем W.
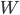Отметим, что число нейронов в каждом скрытом слое для данной модели одинаково и совпадает с числом входных нейронов. Процесс обучения начинается с одного скрытого слоя, если требуемая точность приближения не достигнута, то добавляется следующий слой. Поскольку с добавлением слоя точность приближения растет, то в конечном итоге требуемая точность достигается.

Метод динамического построения ИНС на основе вейвлет-ядра
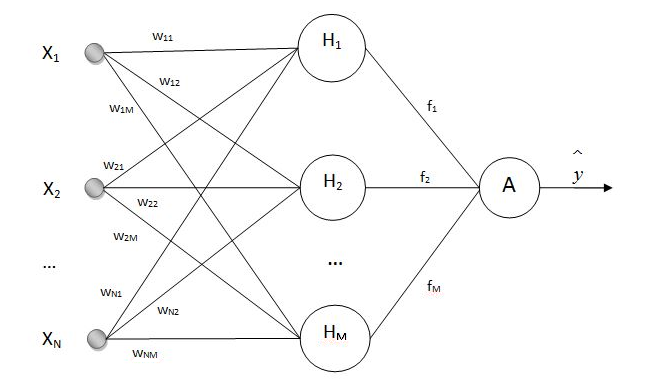
Основное отличие от предыдущей модели заключается в том, что здесь используется один скрытый слой, в котором необходимо подобрать оптимальное число нейронов. Использование в ИНС вейвлет-ядра позволяет не фиксировать функцию 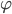\varphi, и делает ИНС достаточно универсальной (рис.2) [11]. Подбор весов осуществляется в результате решения задачи обучения. Задача обучения нейронной сети состоит в вычислении параметров 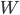W и \{f\}.
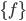Динамическое построение ИНС проводится аналогично динамическому построению ИНС Вольтерра. В случае с ИНС с вейвлет-ядрами процесс построения начинается с исходной ИНС с одним нейроном в единственном скрытом слое. Поскольку с каждым добавлением нейрона точность аппроксимации растет, то через некоторое число шагов мы достигнем требуемой точности аппроксимации.

Выводы
Предложенные модели основаны на теории приближения функции. В первом случае приближается функция от многих переменных с помощью многочлена. Для того, чтобы аппроксимация была успешной, достаточно, чтобы эта функция была определена и непрерывна на компакте 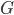G. Компактность достигается применением нормализации, описанной ранее. Во втором случае приближается функция одной переменной вейвлет базисом. Для успешной аппроксимации достаточно, чтобы функция была определена и интегрируема с квадратом на замкнутом интервале.

structura_ins_veivlet

Рис.2. Структура ИНС на основе вейвлет-ядра. Функция активации

Библиографический список

  1. Проблемы Гильберта / под ред. П.С.Александрова. –М.: Наука, 1969. – 240 с.
  2. Колмогоров, А.Н. О представлении непрерывных функций нескольких переменных в виде суперпозиции непрерывных функций одного переменного / А.Н. Колмогоров // Доклады АН СССР. – 1957. – Т.114, № 5. – С. 953-956
  3. Колмогоров, А.Н. О представлении непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных / А.Н.Колмогоров // Доклады АН СССР. – 1956. –Т.108, № 2. –С.179-182.
  4. Арнольд, В.И. О функциях трех переменных / В.И. Арнольд //Доклады АН СССР. – 1957. – Т.114, № 4. – С. 679 – 681.
  5. Hecht-Nielsen,R. Kolmogorov’s mapping neural network existing theorem / R.Hecht-Nielsen // Proceedings of IEEE First annual international conference on neural networks. – San Diego, CA, 1987. –Vol.3. –P.11-14.
  6. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления. В 3 т.Т.3 / Г.М. Фихтенгольц. – М.ФИЗМАТЛИТ, 2008. – 662 c.
  7. Kreinovich, V.Y. Arbitrary nonlinearity is sufficient to represent all functions by neural networks: A theorem / V.Y. Kreinovich // Neural Networks. – 1991. – Vol.4, №3. – P. 381-383.
  8. Gorban, A.N. Approximation of continuous functions of several variables by an arbitrary nonlinear continuous function of one variable, linear functions, and their superpositions / A.N.   Gorban // Appl. Math. Lett. – – Vol.11, №3. – P. 45-49.
  9. Nakamura M. Guaranteed intervals for Kolmogorov's theorem (and their possible relation to neural networks) / Nakamura M., Mines R., Kreinovich V. // Interval Computations. – 1993. – №3. – P.183-199.
  10. Осовский С. Нейронные сети для обработки информации/Пер. с польского И.Д. Изд-во: Финансы и статистика. – – 344 с.
  11. Белявский, Г. И. Нейро-сетевой предсказатель с вейвлет ядром / Г.И. Белявский, И.В. Мисюра // Известия Высших учебных заведений. Северо-Кавказский регион. Естественные науки. – – №3, С.11-14.
  12. Lisheng Yin, Yigang He, Xueping Dong, Zhaoquan Lu Multi-Step Prediction Algorithm of Traffic Flow Chaotic Time Series based on Volterra Neural Network / Lisheng Yin, Yigang He, Xueping Dong, Zhaoquan Lu // Journal of computers. – – Vol. 8, № 6. – P. 1480-1487.
  13. Белявский, Г.И. Алгоритм и программная реализация гибридного метода обучения искусственных нейронных сетей / Г.И. Белявский, Е.В.  Пучков, В.Б.  Лила // Международный журнал "Программные продукты и системы". – Тверь, 2012. – №4. – С. 96-
  14. Vasilis Z. Marmarelis Volterra Models and Three-Layer Perceptrons / Vasilis Z. Marmarelis, Xiao Zhao // IEEE Transactions on neural networks. – – Vol. 8, №6. – P. 1421-1433.
  15. Хайкин С. Нейронные сети: полный курс. – 2-е изд. – М.: Вильямс. – – 1104 с.

 

Опубликовано в: Научно-технический журнал «Вестник Ростовского государственного университета путей сообщения» , Ростов н/Д: РГУПС, №3, 2015.