Алгоритм и программная реализация гибридного метода обучения искусственных нейронных сетей
Авторы статьи: Белявский Г.И., Лила В.Б., Пучков Е.В.
Задача обучения искусственной нейронной сети (ИНС) может рассматриваться как задача оптимизации, при этом основная проблема заключается в выборе среди разнообразных оптимизационных методов наиболее подходящего[2]. Выбор в пользу градиентных методов обоснован тем, что, как правило, в задачах обучения ИНС целевую функцию можно выразить в виде дифференцируемой функции от всех весовых коэффициентов. Однако сложный характер зависимости от весовых коэффициентов приводит к тому, что целевая функция имеет локальные экстремумы и седловые точки, что делает применение градиентных методов не всегда обоснованным. Для решения задач оптимизации с многоэкстремальным критерием используют методы случайного поиска, к которым относятся генетические алгоритмы. Генетические алгоритмы отличаются, как правило, медленной сходимостью. Большего успеха можно достигнуть, используя в одном алгоритме обучения градиентные и генетические методы. Неопределенность выбора метода обучения определяется широким классом градиентных и генетических алгоритмов. В автоматизированных системах нейро-сетевого программирования следует стремиться к сокращению неопределенности. В статье рассматривается параметризация алгоритмов обучения с целью сокращения неопределенности выбора и предлагается соответствующее программное обеспечение.
Общий анализ градиентных методов обучения нейронных сетей позволяет утверждать, что любой из этих методов можно представить как частный случай адаптивного алгоритма[1].
Общую формулу для изменения весов выразим формулой (1):
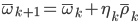 \overline\omega_{k+1} = \overline\omega_k+\eta_k\overline\rho_k , (1)
\overline\omega_{k+1} = \overline\omega_k+\eta_k\overline\rho_k , (1)
где вектор задает направление движения, а - размер шага на k-ой итерации.
Формулу расчета вектора выразим следующим образом:
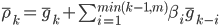 \overline\rho_k = \overline g_k+\sum_{i=1}^{min(k-1,m)} \beta_i \overline g_{k-i} , (2)
\overline\rho_k = \overline g_k+\sum_{i=1}^{min(k-1,m)} \beta_i \overline g_{k-i} , (2)
где вектор 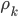 \rho_k задает направление движения;
\rho_k задает направление движения; 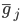 \overline g_j - направление антиградиента на j-ой итерации;
\overline g_j - направление антиградиента на j-ой итерации; 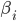 \beta_{i}- коэффициент, определяющий вес i-го градиента; m определяет кол-во запоминаемых градиентов; k – порядковый номер текущей итерации.
\beta_{i}- коэффициент, определяющий вес i-го градиента; m определяет кол-во запоминаемых градиентов; k – порядковый номер текущей итерации.
Градиентный метод обучения из формулы 2 получается при m = 0. А методы сопряженных градиентов[2], которые наиболее часто употребляются при обучении нейронных сетей, получаются путем суммирования всех предыдущих направлений (при m = 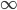 \infty). Параметрами алгоритма являются порядок m и последовательности
\infty). Параметрами алгоритма являются порядок m и последовательности 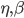 \eta, \beta .
\eta, \beta .
Рассмотрим обучение многослойного персептрона методом обратного распространения с адаптивным алгоритмом минимизации функции ошибки:
- Выбираем начальные значения параметров: стартовую точку
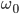 \omega_0, начальное направление движения
\omega_0, начальное направление движения 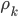 \rho_k, и шаг
\rho_k, и шаг 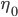 \eta_0.
\eta_0. - Выбираем очередной вектор из обучающего множества и подаем его на вход сети.
- Определяем направление движения
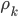 \rho_k по формуле (2).
\rho_k по формуле (2). - Вычисляем критерий остановки, например, среднюю квадратичную ошибку[2,5].
- Если условие остановки выполняется, переходим к шагу 6, если нет – переходим к шагу 2.
- Конец алгоритма. В результате получаем обученную сеть.
Основными недостатками данного алгоритма обучения являются[4]:
- паралич сети;
- попадание в локальные минимумы;
- многократное предъявление всего обучающего множества.
Генетический алгоритм является итерационным, и часто вычисляет решение в некоторой окрестности глобального минимума. В связи с этим он может применяться в задачах подстройки весов при обучении ИНС. К преимуществам генетического алгоритма относится параллельная обработка множества возможных решений для нахождения глобального экстремума многоэкстремальной функции. При этом поиск концентрируется на наиболее перспективных из них.
При обучении ИНС в генетическом алгоритме используются следующие определения[3]:
- ген – весовой коэффициент ИНС;
- хромосома – набор генов (т.е. весовых коэффициентов нейронной сети); каждая хромосома является возможным решением;
- популяция – множество хромосом, вариантов наборов весовых коэффициентов;
- эпоха – итерация, соответствующая созданию нового поколения хромосом.
Хромосомы являются основными сущностями, над которыми в определенном порядке в пределах одной эпохи проводятся следующие операции:
- скрещивание – создание с определенной степенью вероятности (Pс) новой хромосомы из генов двух других и добавление ее в популяцию;
- мутация – изменение с определенной степенью вероятности (Pm) значения произвольного гена любой хромосомы и добавление ее в популяцию;
- приспособление – удаление из популяции хромосом (т.е. наборов весовых коэффициентов), показавших худший результат.
Мутация при обучении ИНС необходима, так как она позволяет выходить популяции из локального экстремума, а также является способом получения новых более здоровых особей.
На рис.1 показана ИНС типа многослойный персептрон. Хромосома составляется из весовых коэффициентов в порядке слева направо, сверху вниз.
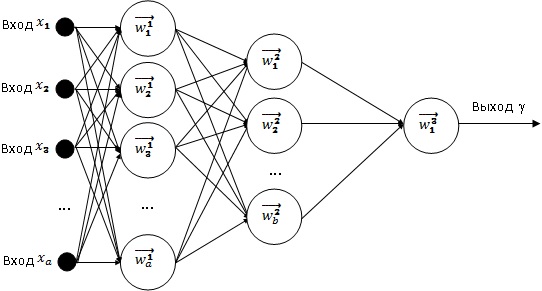 Рис. 1. ИНС, тип многослойный персептрон
Рис. 1. ИНС, тип многослойный персептрон
Таким образом, хромосома представляет собой набор генов – весовых коэффициентов[3]:
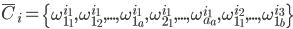 \overline C_i = \left\{ \omega_{1_{1}}^{i_1}, \omega_{1_{2}}^{i_1}, ..., \omega_{1_{a}}^{i_1}, \omega_{2_{1}}^{i_1}, ..., \omega_{a_{a}}^{i_1}, \omega_{1_{1}}^{i_2}, ..., \omega_{1_{b}}^{i_3} \right\} , (3)
\overline C_i = \left\{ \omega_{1_{1}}^{i_1}, \omega_{1_{2}}^{i_1}, ..., \omega_{1_{a}}^{i_1}, \omega_{2_{1}}^{i_1}, ..., \omega_{a_{a}}^{i_1}, \omega_{1_{1}}^{i_2}, ..., \omega_{1_{b}}^{i_3} \right\} , (3)
где C – хромосома, i – индекс представителя популяции, 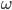 \omega – вес нейрона.
\omega – вес нейрона.
Так как генетический алгоритм не является строго детерминированным, существует возможность производить скрещивание и мутацию в произвольном порядке в пределах одной эпохи. Выбор пар для скрещивания (Ga, Gb). Хромосома выбирается для скрещивания с вероятностью пропорциональной результату. Для каждого гена новой хромосомы присваиваем ген либо хромосомы Ga, либо хромосомы Gb с вероятностью 0,5:
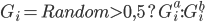 0,5 ? G_{i}^a : G_{i}^b " /> G_i = Random > 0,5 ? G_{i}^a : G_{i}^b , (4)
0,5 ? G_{i}^a : G_{i}^b " /> G_i = Random > 0,5 ? G_{i}^a : G_{i}^b , (4)
где Gi – ген новой хромосомы, Ga и Gb – гены родительских хромосом, i – порядковый номер гена в хромосоме, Random – функция, генерирующая равномерную случайную величину на отрезке действительных чисел [0;1].
Для каждой особи популяции с вероятностью Pm (как правило, Pm = 0,2) определим особей, подлежащих мутации. Для каждого гена выбранной особи с вероятностью Pg произведем мутацию.
Для мутации гена воспользуемся формулой (5):
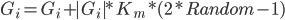 G_i = G_i + |G_i| * K_m * (2 * Random - 1), (5)
G_i = G_i + |G_i| * K_m * (2 * Random - 1), (5)
где Gi – ген хромосомы, i – порядковый номер гена в хромосоме, Random – функция, генерирующая равномерную случайную величину на отрезке действительных чисел [0;1], Km – коэффициент мутации (как правило, 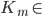 K_m \in [0;1]).
K_m \in [0;1]).
Таким образом, к параметрам генетического алгоритма относятся размер популяции, число потомков, число хромосом для мутаций, вероятности выбора хромосомы и вероятность мутации гена. Соответствующий подбор параметров позволяет выделить генетический алгоритм из широкого класса алгоритмов.
Для гибридного обучения ИНС получаем 2 альтернативы. В первом случае будем начинать обучение адаптивным алгоритмом и, достигнув критерия перехода, будем продолжать обучение генетическим алгоритмом, добавив к первой популяции здоровую особь – ИНС, обученную адаптивным алгоритмом.
Критериями перехода от адаптивного к генетическому методу обучения для гибридного алгоритма являются:
- Количество эпох обучения A.
- Среднеквадратическая ошибка E.
Второй альтернативной реализацией гибридного алгоритма будет обучение ИНС генетическим алгоритмом. В результате работы генетического алгоритма будет получена популяция, наилучший представитель которой является одним из возможных решений задачи обучения. Если значение критерия обучения удовлетворяет заданному качеству, то можно считать, что процесс обучения завершен. Если это не так, то будем продолжать обучение адаптивным алгоритмом.
Критериями перехода от генетического к адаптивному методу для второго варианта гибридного алгоритма являются:
- Количество эпох обучения A.
- Среднеквадратическая ошибка E.
- Стационарность популяции.
Рассмотрим алгоритм предлагаемого гибридного метода обучения варианта «адаптивный + генетический»:
- Создаем ИНС с первоначальной инициализацией весовых коэффициентов.
- Обучаем ИНС описанным выше адаптивным алгоритмом, пока не будет достигнут критерий перехода к генетическому методу обучения.
- Создаем популяцию из N-1 особей. В первую популяцию добавим ИНС, обученную адаптивным алгоритмом.
- Произведем скрещивание особей с вероятностью выбора пары Pc. От каждой пары получим S потомков. Для определения генов потомка, воспользуемся формулой (4).
- Выберем из новой популяции лучших N особей.
- Если лучший представитель особи соответствует заданному качеству обучения, то переходим к шагу 9.
- Произведем мутацию для особей, выбранных с вероятностью Pm. Для каждого гена выбранной особи с вероятностью Pg произведем мутацию. Для мутации гена воспользуемся формулой (5).
- Если лучший представитель особи соответствует заданному качеству обучения, то переходим в шагу 9, нет – возвращаемся к шагу 4.
- Конец алгоритма. В результате получаем обученную сеть (лучший представитель особи).
Окончательный выбор алгоритма обучения зависит от конкретной задачи. Поэтому для тестирования алгоритмов был реализован эмулятор искусственной нейронной сети в виде веб-приложения. Язык программирования выбран PHP.
На рис.2 приведена диаграмма классов методов обучения реализованного программного продукта.
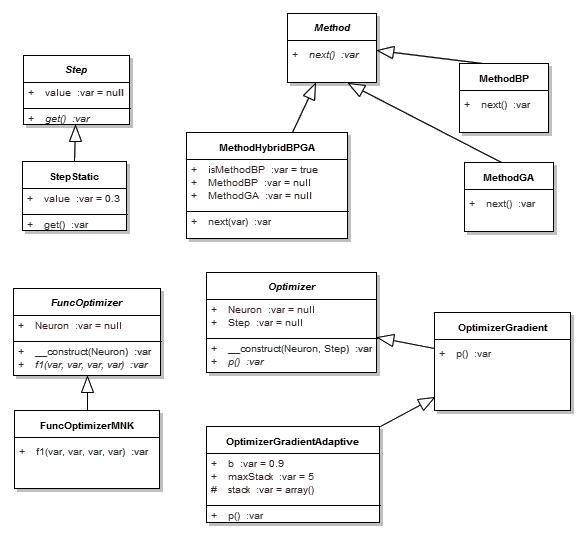 Рис. 2. Диаграмма классов механизма обучения ИНС
Рис. 2. Диаграмма классов механизма обучения ИНС
Родителем для всех классов-методов обучения является abstract class Method. Основными потомками данного класса являются классы:
- метод обратного распространения ошибки – class MethodBP;
- генетический метод обучения – class MethodGA;
- гибридный метод обучения – class MethodHybridBPGA.
Гибридный метод инкапсулирует в себе два объекта методов:
- class MethodBP;
- class MethodGA.
Алгоритмы оптимизации функции ошибки представлены классами:
- абстрактный класс Optimizer;
- класс OptimizerGradient – реализует поиск минимума методом простого градиентного спуска;
- класс OptimizerGradientAdaptive – реализует поиск минимума адаптивным методом.
Функция ошибки нейрона представлена классом FuncOptimizerMNK, который реализует функцию наименьших квадратов.
На рис. 3 изображена диаграмма основных классов архитектуры ИНС.
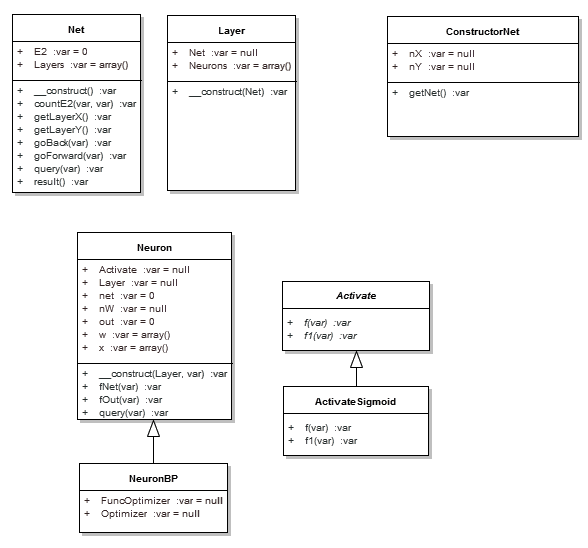 Рис. 3. Диаграмма основных классов архитектуры ИНС
Рис. 3. Диаграмма основных классов архитектуры ИНС
Архитектура многослойного персептрона реализована классами Net, Layer, Neuron, и дополнительным классом нейрона – NeuronBP, который применяется в методе обратного распространения ошибки. В отличие от класса Neuron, он заключает в себе функцию ошибки и алгоритм оптимизации функции ошибки.
Классы Activate и ActivateSigmoid реализуют активационную функцию нейрона. В данном случае – сигмовидную.
Были проведены эксперименты с обучением искусственной нейронной сети топологии многослойный персептрон. В качестве задачи для обучения была выбрана задача аппроксимации двумерной функции Розенброка[5], x,y  \in [0;3]. Обучающая выборка состояла из 155 примеров, размер входного вектора - 2, выходного – 1. Критериями остановки обучения были: порог в 1000 эпох и среднеквадратическая ошибка, составляющая 0,001.
\in [0;3]. Обучающая выборка состояла из 155 примеров, размер входного вектора - 2, выходного – 1. Критериями остановки обучения были: порог в 1000 эпох и среднеквадратическая ошибка, составляющая 0,001.
Для экспериментов создано 10 ИНС. В анализе участвовали следующие алгоритмы: простой градиентный спуск, адаптивный алгоритм, генетический алгоритм, «адаптивный + генетический», «генетический + адаптивный». Результаты исследования представлены в таблицах 1 и 2.
Таблица 1.Результаты исследования алгоритмов обучения ИНС
| № | Методы оптимизации | |||||||||
| Градиентный спуск | Адаптивный алгоритм | Генетический | Адаптивный + Генетический | Генетический + Адаптивный | ||||||
| Ошибка | Кол-во эпох | Ошибка | Кол-во эпох | Ошибка | Кол-во эпох | Ошибка | Кол-во эпох | Ошибка | Кол-во эпох | |
| 1 | 0,003017 | 1000 | 0,001103 | 1000 | 0,000999 | 760 | 0,000906 | 613 | 0,001124 | 1000 |
| 2 | 0,001434 | 1000 | 0,001099 | 1000 | 0,000993 | 480 | 0,000985 | 737 | 0,001158 | 1000 |
| 3 | 0,001474 | 1000 | 0,001122 | 1000 | 0,001019 | 1000 | 0,000978 | 400 | 0,001293 | 1000 |
| 4 | 0,001778 | 1000 | 0,001137 | 1000 | 0,000990 | 723 | 0,001069 | 1000 | 0,001102 | 1000 |
| 5 | 0,001456 | 1000 | 0,001115 | 1000 | 0,000992 | 624 | 0,000980 | 435 | 0,001145 | 1000 |
| 6 | 0,001426 | 1000 | 0,001105 | 1000 | 0,000971 | 781 | 0,000991 | 955 | 0,001127 | 1000 |
| 7 | 0,001420 | 1000 | 0,001144 | 1000 | 0,000997 | 553 | 0,000959 | 654 | 0,001161 | 1000 |
| 8 | 0,001418 | 1000 | 0,001133 | 1000 | 0,000982 | 602 | 0,001053 | 1000 | 0,001108 | 1000 |
| 9 | 0,001418 | 1000 | 0,001183 | 1000 | 0,000990 | 704 | 0,000998 | 685 | 0,001282 | 1000 |
| 10 | 0,001571 | 1000 | 0,001229 | 1000 | 0,015316 | 1000 | 0,001129 | 1000 | 0,001183 | 1000 |
Таблица 2. Сравнительные характеристики процесса обучения рассмотренных алгоритмов
| Алгоритм обучения | Время одной эпохи (в миллисекундах) | худший результат | лучший результат | ||
| число эпох | ошибка | число эпох | ошибка | ||
| Простой градиентный спуск | 60 | 1000 | 0,003017 | 1000 | 0,001418 |
| Адаптивный алгоритм | 120 | 1000 | 0,001229 | 1000 | 0,001099 |
| Генетический алгоритм | 220 | 1000 | 0,015316 | 480 | 0,000993 |
| Гибридный алгоритм («адаптивный + генетический») | ~160 | 1000 | 0,001129 | 400 | 0,000978 |
| Гибридный алгоритм («генетический + адаптивный») | ~180 | 1000 | 0,001293 | 1000 | 0,001103 |
В результате проведенных экспериментов видно, что с задачей справились генетический алгоритм и гибридный алгоритм версии «адаптивный + генетический». Как показывает эксперимент, для данной задачи обучения быстрее всего сходились градиентные методы, но до определенной среднеквадратической ошибки, в среднем до 0,003. Порог в 0,001 за 1000 эпох не преодолел ни один градиентный метод. Из этого следует, что целесообразнее всего в начале обучения использовать адаптивный метод, который достаточно быстро находит решение со среднеквадратической ошибкой 0,003, а далее – применять генетический алгоритм.
По экспериментам видно, что по количеству эпох генетический алгоритм в некоторых случаях быстрее гибридного. Но для данной задачи время одной эпохи генетического алгоритма гораздо выше (220 миллисекунд), чем среднее время одной эпохи гибридного (160). Поэтому, можно сделать вывод, что лучше всего для данной задачи подходит гибридный алгоритм варианта «адаптивный+генетический».
Таким образом, получена параметрическая модель обучения ИНС, содержащая широкий спектр известных алгоритмов обучения и позволяющая настроить параметры, чтобы наилучшим образом решить поставленную задачу.
Список использованной литературы:
- Лила В. Б. Алгоритм и программная реализация адаптивного метода обучения искусственных нейронных сетей. – Инженерный вестник Дона. 2012 г.
- Тархов Д.А. Нейронные сети. Модели и алгоритмы. Кн.18. Справочное издание. (Серия 'Нейрокомпьютеры и их применение'): – М.: Радиотехника, 2005. – 256с.
- Липанов А.М. Применение генетического алгоритма для обучения нейронной сети в задаче идентификации СТМ – изображений. Липанов А.М., Тюриков А.В., Суворов А.С., Шелковников Е.Ю., Гуляев П.В. - Ползуновский вестник. – 2010. – №2. – С.217-221.
- Хайкин С. Нейронные сети: полный курс, 2-е издание. : Пер. с англ. – М. : Издательский дом «Вильямс», 2006. – 1104 с.: ил. – Парал. тит. англ.
- Гришин А. А., Карпенко А. П. Исследование эффективности метода пчелиного роя в задаче глобальной оптимизации. – Электронное научно-техническое издание «Наука и образование». 2010г.
Опубликовано в: Международный журнал "Программные продукты и системы", Тверь, №4, 2012, с. 96 - 100.


